凯利公式(清晰实用的凯利公式运用举例)
交易真经按:“凯利公式” 无疑是投资界应用最广泛的风险收益平衡计算方法之一,但是网络上很难找到比较实用的说明资料,本文从实用角度举例介绍它在交易中的运用。
本文附有最优仓位计算实例
一、“凯利公式” 不是闹着玩的
“凯利公式” 的应用要从爱德华 · 索普说起,国内许多朋友对这个名字比较陌生,他不仅是中性策略的开创人,也是第一个通过数学战胜赌场的人。
索普究竟有多牛?就连比尔 · 格罗斯也深受他的影响,尊称索普为自己的恩师。这里顺带介绍格罗斯这位自称 “容易受伤的男人”,他管理的资金规模近万亿美元,是巴菲特的四倍,也是唯一一位三次被晨星评为 “最佳固定收益基金经理人” 的人。(晨星是国际基金评级的权威)
索普不但是格罗斯心目中的恩师,也是金融界许多大名鼎鼎的投资大师心中的 “教父” 人物,以及量化投资真正的“开山鼻祖”。
他 1969 年创立的基金年均复合增长率高达 20%,不仅保持每年不亏钱,甚至每个月都不亏钱。这是金融历史上第一个真正意义上的依靠数学模型和量化算法策略赚钱的投资基金。
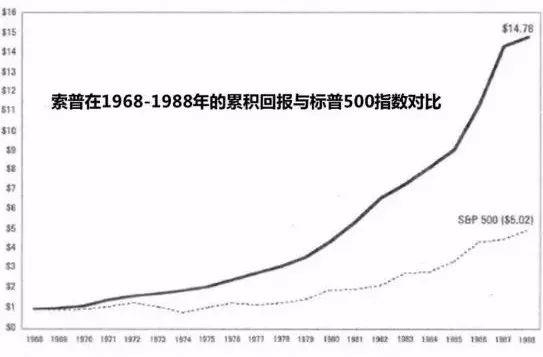
重点是,索普将凯利公式应用到他的资金管理上。这么长的铺垫也是为了说明 “凯利公式” 不是闹着玩的。
巴菲特的投资组合也完美地结合了凯利公式,既然世界上众多著名的投资大师们都在使用凯利公式,那么在实际交易中它到底有哪些参考价值呢?
二、“凯利公式” 的清晰说明
1956 年,凯利公式出自物理学家凯利之手,后来被他的朋友的朋友-索普先生率先运用于赌博和股票交易上,并且取得巨大成功。
它最简洁的表达式是:f=(pb-q)/b,计算的过程比较复杂,现在看不懂没关系,在后面会结合策略一步步解释清楚的。首先认识一些常见的策略名词的概念。
我们以 “抛硬币赌局” 进行名词解释。假设每次的押注额是 100 元,正面 / 赢 300 元,反面 / 亏 100 元。(即:押对了连押注的本金和盈利总共 300 元,如果押错了就只赔掉 100 元本金)
**1、胜率(p):**是指获胜的概率。因为出正面的概率是 50%,所以胜率是 0.5。
**2、败率(q):**是指失败的概率。因为出反面的概率也是 50%,所以败率也是 0.5。
获胜的机会 + 失败的机会=100%
胜率 p=100%- 败率 (即:p=1-q)
败率 q=100%- 胜率 (即:q=1-p)
**净赔率(b):**是指减去押注本金之后的净收益是本金的多少倍。如果赢了可以获得 300 元,但是其中有 100 元押注本金,所以实际只赚了 200 元,所以净赔率为 2。
净赔率=(赢得总额 - 押注本金)/ 押注本金
**3、赢面:**期望净收益率,指重复博弈的胜算机会有多大。赢面小于 0 或者等于 0 的博弈是不值得参与的。计算赢面的方法是:净赔率 * 胜率 - 败率,以上抛硬币赌局的赢面是 2*0.5-0.5=0.5。
赢面=净赔率 * 胜率 - 败率 (即:b*p-q)
**4、凯利公式:**在一个期望净收益为正的独立重复赌局中(即赢面大于 0 的博弈)计算出获得长期总本金增长率最大化的投注比例,算法如下:
最佳仓位 (f)=((净赔率 * 胜率)- 败率)/ 净赔率
即:f=(pb-q)/b
**还是以上面的抛硬币为例:**为了更贴近实际交易的效果,假设本金 1 万元,每次最小下注额度要求是 100 元,大于 100 元的可以不按 100 的整数倍下注。那么这个赌局的最优下注比例计算方法如下:
最佳仓位 (f)=((净赔率 * 胜率)- 败率)/ 净赔率
最佳仓位 (f)= 赢面 / 净赔率
最佳仓位 (f)=( (2*0.5)-0.5 ) / 2
最佳仓位 (f)=25%
为什么 25% 才是最优投注比例?虽然这是一个赢面很高的赌局,但是如果每次使用 100% 的本金押注(满仓),只要中途错一次就会面临爆仓出局,显然满仓操作是很糟糕的做法;如果只使用 1% 的仓位那么资金利用率又太低了;
事实证明仓位过重或者过轻都不是最优解。只有按照凯利公式计算的比例下注才是最优的,既可以保证中途不会爆仓出局,又保证了长期玩下去能赢到最多的钱。
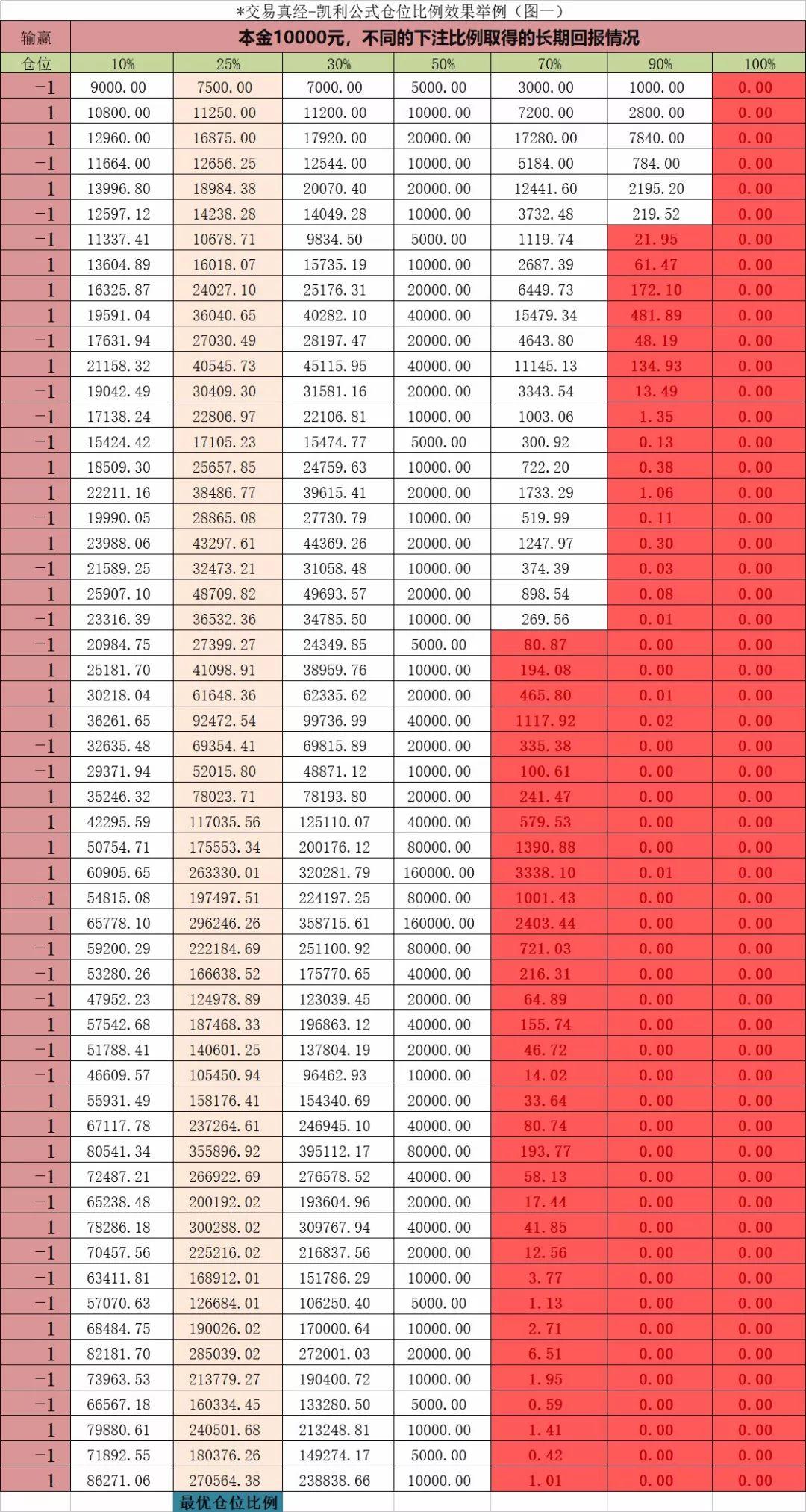
上图中,浅黄色这栏就是按照凯利公式进行投注的结果,随着重复博弈的次越多,它的总收益也是最高的;而红色区域显示仓位越大就越容易过早爆仓出局。没错,从数学理论的角度看凯利公式就是这么牛逼哄哄!
三、凯利公式在交易策略中的计算方法
股票 / 期货 / 外汇等交易与赌博不同的地方主要有以下两个方面:
**1、不同策略的胜率差异很大。**比如有的策略虽然胜率只有 20%,但是却是优秀的策略;
2、对于每次交易的持仓资金,并非是要么盈利要么全部亏完。使用凯利公式之前,重点要搞明净赔率在实际策略中对应的涵义。
**策略净赔率计算举例:**无论总本金的大小,我们只需要按照每次交易的实际建仓资金额计算即可。比如每次操作的盈利预期是 30%、止损预期是 - 10%,那么相当于每次交易都是使用 10% 的风险预期换取 30% 的收益预期。将每次交易的亏损预期看作一个份额的赌注,假如当次交易做对了账户里会赚到三份额的钱;如果做错了账户里就会减少了这一个份额的钱。因为做对了账户里不但不会减少下注的这份钱,另外还多出了盈利的三份钱,所以净赔率实际上就是指策略的盈亏比。净赔率=盈亏比
**关于策略净赔率的计算举例:**已知策略过去十年期间的胜率是 64.34%、盈亏比是 2.02,我们可以通过以下几个值求出最优的理论仓位比例:胜率(p)=64.34%
败率(q)=1-64.34%=35.66% 净赔率(b)=2.02
f=( (净赔率 * 胜率)- 败率 )/ 净赔率
=(2.02*0.6434-0.3566)/2.02
=0.4669
即: 该策略的理论最优仓位比例是 46.69%

上图是该策略以 50 万为初始本金,按照 46.69% 仓位比例进行交易的权益增长情况。(由于数据很长,所以有部分截图)
四、看得见的是概率、看不见的是陷阱
何鸿燊接手葡京不久赌场生意蒸蒸日上,理性的他有些顾虑,于是请教 “赌神” 叶汉。
鸿燊:如果这些赌客总是输钱,时间长了,他们都不来赌了怎么办?叶汉:一次赌徒,一生赌徒。他们更加担心你的赌场不开了怎么办。叶汉的回答深刻反映了投机学中的人性层面,但是赌徒永远不明白,打败他们的不是人性而是概率。大的投资机构在评估投资风险与长期收益的平衡时,会参考凯利方程式的原理,而巴菲特则对凯利公式进行了优化。巴版凯利公式如下:x=2*p-1p=成功的概率
x=投入的资金百分比
这些就是投资与数学紧密相关的最好的说明。
**普通交易者看不见的陷阱:**通过凯利公式计算头寸比例,当然是最优解。但是只懂得 f 值的计算方法,却没有经验和能力保证 p 值和 b 值也是可靠的,那么整个方程就就完全失去了它的意义。像巴菲特这样的投资大师,必然有自己的完善的情报研究系统、价值评估系统以及完善的产品对冲体系等。从长期角度看,他们对方程中 p 值和 b 值的把握度远比普通交易者优胜得多,这就是为什么大师们能运用好凯利公式的根本原因。真正的陷阱不在于凯利公式本身,而在于普通交易者对策略缺乏整体的逻辑思考和论证能力。显然,无法平衡好系统中其它必要的变量,无论什么方程都会变成交易途中的 “陷阱”。